|
Knight's Tours
Advisor: Mark Krusemeyer
Authors: Rob Gaebler, Tsu-wang Yang
Date: August 13, 1999
| 
|
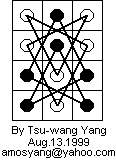
A standard chessboard, as most people know, is 8 squares by 8 squares. The knight, one of the pieces in the game of chess, moves in the following peculiar way: It moves two spaces in one of the four directions, then one space perpendicular to the first direction (this is considered one move, not two separate moves), like this:
Two interesting problems that arise from the way the knight moves are these: Can the knight start on a square of the chessboard, and visit every space on the chessboard exactly once, without missing a square and without stepping on the same square twice? This is called an open tour of the chessboard. If an open tour is possible, is it also possible to move from the last square visited back to the first square in a single move? This is called a closed tour of the chessboard.
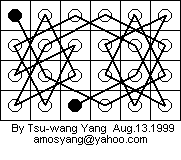
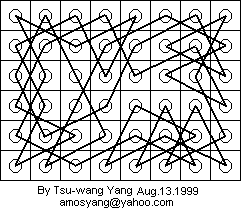
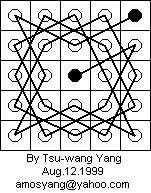
As the following diagram shows, both anwers are "Yes" for the 8 x 8 chessboard.
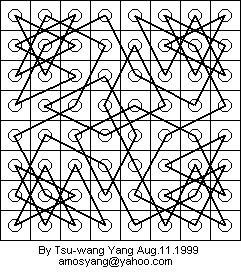
Since a closed tour implies an open tour, only an example of a closed tour is needed.
The next important question is this: For what dimensions m x n of a chessboard does an open tour exist? What about a closed tour? These two questions are the basis of this entire project. The results are summarized here, with a full proof following.

By examination, the first two lists are mutually exclusive and include all boards, as are the last two lists. (Note: It is not assumed that m <= n; an m x n tour implies a n x m tour, and vice versa.)
Proof (Closed Tours):
First, the trivial cases 1 x n and 2 x n are obvious. I will not go into a useless debate over whether the 1 x 1 board should be considered a closed tour.
Second, m x n boards where m and n are both odd. Consider the colors of the squares of the board (they form an alternating pattern, as on the regular chessboard). Every time the knight moves, it moves to a square of the opposite color. In a closed tour, the last move is back to the first square of the tour. Since the color of the square the knight was on changed each time it moved, and it ended on the same color square, it must have moved an even number of times. But since m and n are both odd, the total number of squares, mn, is odd, so the knight must have moved an odd number of times. It is very difficult for a knight to move an even and an odd number of times simultaneously.
Third, 4 x n boards. Color the board in the following way:
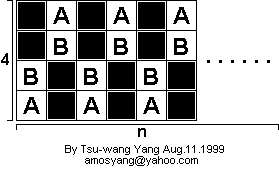
From each of the white squares labeled A, the knight can only move to a white square labeled B. There are n A squares and n B squares. Suppose there were a closed tour. Then there would be 2n moves to/from an A square, and 2n moves to/from a B square. But 2n of the moves to/from B squares are also to/from A squares. So there is never a move from a B square, and therefore any white square, to/from any black square. So the black squares never get visited, and there is no closed tour.
Fourth, the 3 x 4 board. Consider the following diagrams:

A must be connected to F and C, as those are the only two squares accessible from A. We'll say that AC and AF are "moves" in the closed tour. Likewise, EB, EC, BD, and DF are all moves in the closed tour. But these moves form a closed loop that does not contain all the squares of the board. (From now on, we'll say "closed loop" to refer to a series of moves that ends on the square it started, but doesn't contain all the squares of the chessboard.) So there is no closed tour on the 3 x 4 chessboard.
Fifth, the 3 x 6 board. Consider the following diagrams:

All squares A must connect to all squares B. But we then have a closed loop. So there is no closed tour.
Sixth, the 3 x 8 board. Consider the following diagrams:
Assume there is a closed tour. Right away, we know several moves that must be in the tour (whenever a square has only two moves available to it). But we can figure out even more about what the tour must look like.
BK and PK are not both moves in the tour; otherwise, there would be the closed loop APKBOJA. Without loss of generality, say BK isn't a move in the tour. Then BQ must be.
PC is not a move in the tour; otherwise, BQHCPKB would be a closed loop. So PK is a move.
LF and LT are not both moves in the tour; otherwise, LFUMGTL would be a closed loop. So LC is a move in the tour.
Finally, DS and RE are both moves in the tour, since nothing other than E and S are accessible to R and D, respectively. But now IDSNERI is a closed loop. Since this was a construction of a general closed tour given the assumption that one existed, there is no closed tour on the 3 x 8 board.
Now we prove that there is a closed tour for all other m x n boards. First, notice the following boards with closed tours:
| 3x10
| 3x12
|

|
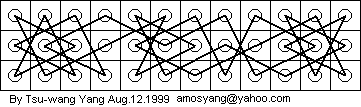
|
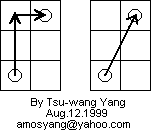
Consider the following 3 x 4 open tour:

This board can be "glued" to any 3 x n closed tour to make a 3 x (n + 4) closed tour. This does indeed result in a closed tour. Consider the step where the knight moves into the corner of the 3 x n board during its closed tour. If the knight were to instead jump off the board (onto the 3 x 4 board), jump around a little bit, then hop back on the 3 x n board and continue on its way, it would complete a loop that visited every square on both boards exactly once, and end back where it started. But that is the definition of a closed tour. So there exists a 3 x (n + 4) closed tour. Here's what it looks like, using this method:
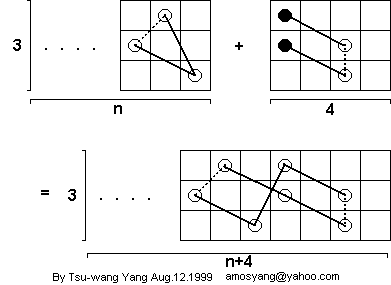
In the diagram, the dotted lines indicate that two squares are connected by a series of moves, but not directly, in a tour.
Now comes the inductive step. Assume a 3 x n closed tour exists. Then a 3 x (n + 4) closed tour also exists, and can be constructed as shown above. 3 x 10 and 3 x 12 closed tours exist (and are shown above). Therefore a 3 x n closed tour exists if n >= 10, even. Such a tour can be constructed by gluing the above 3 x 4 open tour to a closed 3 x 10 or 3 x 12 closed tour a certain number of times:

Consider these open tours:
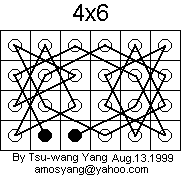
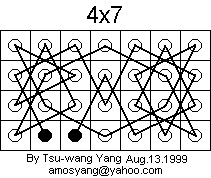
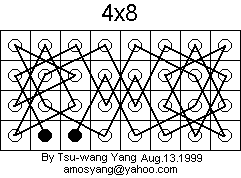
Now consider the following 3 x 4 board without a tour, but with two closed loops:
This board can be added to any 4 x n open tour to make a 4 x (n + 3) open tour, and the two end squares of the resulting tour are the same as in the 4 x n tour. Here's what the new tour looks like:

In the diagram above, it is assumed that the two end squares of the 4 x n open tour are not in the right three columns. Thus the 4 x 6, 4 x 7, and 4 x 8 open tours shown above meet this criterion. By induction, there exists a 4 x n open tour, n >= 6, with the two end squares near the lower left, as in the examples above.
Such a 4 x n open tour can be added to an m x n closed tour to get a (4 + m) x n closed tour:
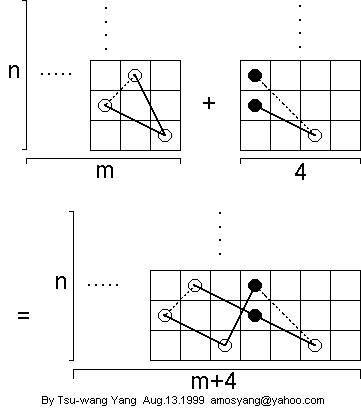
Now we are ready for the final touch. Consider these closed tours:
| 6x5
| 6x6
|

| 
|
| 6x7
| 6x8
|

| 
|
| 8x5
| 8x6
|
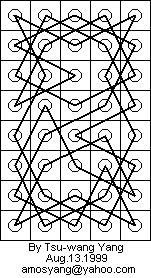
| See 6x8
|
| 8x7
| 8x8
|

| 
|
Now we apply the inductive argument four times:
A 6 x n closed tour exists, n >= 5.
(Base cases: 6 x 5, 6 x 6, 6 x 7, and 6 x 8 closed tours.)
An m x n closed tour exists, m = 6 + 4k, k = 0, 1, 2, ...; n >= 5.
(Base cases: 6 x n closed tour, n >= 5.)
An 8 x n closed tour exists, n >= 5.
(Base cases: 8 x 5, 8 x 6, 8 x 7, and 8 x 8 closed tours.)
An m x n closed tour exists, m = 8 + 4k, k = 0, 1, 2, ...; n >= 5.
(Base cases: 8 x n closed tour, n >= 5.)
Combining these, we get that an m x n closed tour exists, m >= 6, even; n >= 5.
All boards have now been classified conclusively as having a closed tour or having no closed tour. The proof is complete.
Proof (Open Tours):
Just as for closed tours, 1 x n and 2 x n boards obviously do not have open tours. The 3 x 3 board also contains no open tour. Consider the center square. There is no way for the knight to move to/from that square, so there is no open tour.
The 3 x 5 board does not have an open tour. Consider the following diagram:
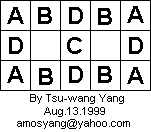
Suppose an open tour exists for the 3 x 5 board. Then the A squares can only be connected to B and C squares. But only two squares can be connected to C. So two A squares are the ends of the open tour. But then the four D squares form a closed loop. So there is no 3 x 5 open tour.
The 3 x 6 board does not have an open tour. Consider the following diagram:
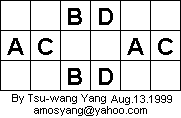
Suppose an open tour exists for the 3 x 6 board. Then one of the A squares is an end of the tour; otherwise we would have a closed loop ABABA. Similarly, one of the C squares is an end of the tour; otherwise we would have a closed loop CDCDC. So there is no 3 x 6 open tour.
The 4 x 4 board, surprisingly, has no open tour. Consider the following diagram:
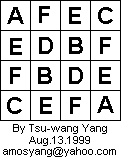
Suppose an open tour exists for the 4 x 4 board. The A squares can only be connected to B squares. One of the A squares is an end of the tour; otherwise we would have a closed loop ABABA. Similarly, one of the C squares is an end of the tour; otherwise we would have a closed loop CDCDC. So there are three moves AB and three moves CD. This leaves one move BX, where X is E or F, and one move DX. So there is a total of two moves XY, where Y is B or D. But there must be two moves EY; otherwise, we have a closed loop EEEE. Similarly, there must be two moves FY; otherwise, we have a closed loop FFFF. But this makes a total of four moves XY, and 2 does not equal 4. So there is no 4 x 4 open tour.
Now all that is left is to prove that the list of open tours that do exist is correct.
Consider these open tours:
Now consider the following 3 x 4 open tour.
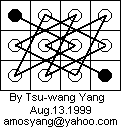
If a 3 x n board has an open tour that ends on a corner square, this 3 x 4 open tour can be added to the 3 x n open tour, and the result will be a 3 x (n + 4) open tour that ends on a corner square. Here's what the new tour looks like:
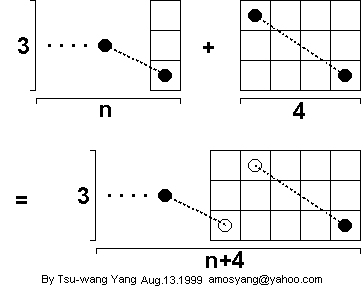
In the diagram above, it is assumed that the left end square of the 3 x n open tour is not in the right column. It could be anywhere else, though. Thus the 3 x 7, 3 x 8, 3 x 9, and 3 x 10 open tours shown above meet this criterion. By induction, there exists a 3 x n open tour, n >= 7, with an end square in the corner.
Consider these open tours:
Recall the argument that said that the following 3 x 4 board could be added to a 4 x n open tour, and the result would be a 4 x (n +3) open tour with the end squares the same as before:

The 4 x 6, 4 x 7, and 4 x 8 open tours shown above meet the criterion that the two end squares are not in the right three columns. So by induction, there exists a 4 x n open tour, n >= 5, with the two end squares in the same positions as in the examples above.
If an m x n board has an open tour that ends on a corner square, this 4 x n open tour can be added to the m x n open tour, and the result will be a 3 x (n + 4) open tour that ends on a corner square. Here's what the new tour looks like:
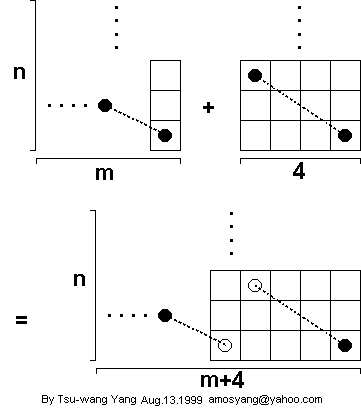
Now consider these open tours:
| 5x5
| 5x7
|
| 
|
We apply the inductive argument four times:
A 5 x n open tour exists, n >= 5, odd.
(Base cases: 5 x 5 and 5 x 7 open tours.)
An m x n open tour exists, m = 5 + 4k, k = 0, 1, 2, ...; n >= 5, odd.
(Base cases: 5 x n open tour, n >= 5.)
A 7 x n open tour exists, n >= 5.
(Base cases: 7 x 3 and 7 x 5 open tours.)
An m x n open tour exists, m = 7 + 4k, k = 0, 1, 2, ...; n >= 3, odd.
(Base cases: 7 x n open tour, n >= 3.)
Combining these, we get that an m x n open tour exists, m >= 5, odd; n >= 5, odd. If we use the results from the closed tours (an m x n closed tour exists for m >= 5; n >= 6, even), we get that an open m x n tour exists for m >=5, n >= 5. But we have shown that a 4 x n open tour exists, n >= 5. So an m x n open tour exists for m >=4, n >=5. This concludes the proof.
p.s. We made a program to help find tours on certain large boards (8x8, 7x8, etc. you don't want to do it by hand) in C++. E-mail to amosyang@yahoo.com if you are interested in finding out more about this program. :)